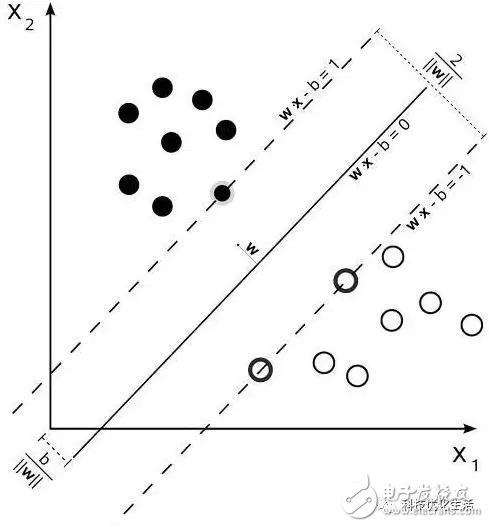
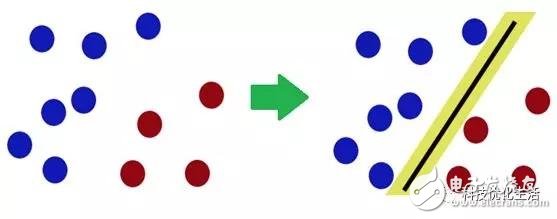
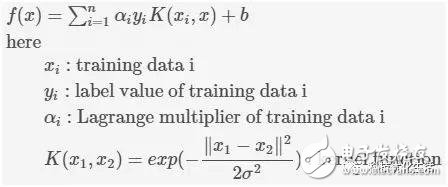There are five major schools of artificial intelligence machine learning: 1) symbolism, 2) Bayesian, 3) connectionism, 4) evolutionism, 5) Analogizer. Today we focus on the best algorithm in Algorithmizer - Support Vector Machine (SVM) SVM overview: The Support Vector Machine (SVM) is a new and very promising classification technique proposed by the AT&T Bell Laboratory Research Group led by Vapnik in 1995. At the beginning, it was mainly proposed for the binary classification problem, and successfully applied the sub-solution regression and a classification problem, and extended it to the multi-value classification problem that exists in a large number of applications. Support Vector Machine (SVM) is a supervised learning model related to related learning algorithms. Since its inception, Support Vector Machine (SVM) has swept the field of machine learning due to its good classification performance, and has firmly suppressed the field of neural networks for many years. If the integrated learning algorithm is not considered, regardless of the specific training data set, the performance SVM in the classification algorithm can be said to be the first. Support vector machine (SVM) has many unique advantages in solving small sample, nonlinear and high-dimensional pattern recognition, and can be applied to other machine learning problems such as function fitting. Introduction to SVM principle: The support vector machine (SVM) method is based on the VC dimension theory and structural risk minimization principle of statistical learning theory. It seeks the best compromise between the complexity and learning ability of the model based on the limited sample information. The best promotion ability. Support vector machines (SVMs) are similar to neural networks and are learning mechanisms, but unlike neural networks, SVM uses mathematical methods and optimization techniques. The mathematical theoretical basis behind the SVM (probability theory and mathematical statistics, functional analysis and operations research, etc.) is a great mathematical achievement of modern humans. Due to the difficult mathematics, SVM research has not received sufficient attention. Until the implementation of the statistical learning theory SLT and the research of the more emerging machine learning methods such as neural networks encountered some important difficulties, the SVM was rapidly developed and improved. Support Vector Machines (SVM) can analyze data, identify patterns, and use for classification and regression analysis. Given a set of training samples, each marked as belonging to two categories, an SVM training algorithm builds a model, assigning new instances to one class or other classes, making it a non-probabilistic binary linear classification. An example of an SVM model, such as points in space, maps so that the examples of the different categories are represented by a distinct gap that is as broad as possible. The new embodiment maps to the same space and predicts that they belong to a category based on their falling on the gap side. In addition to linear classification, support vector machines can use kernel techniques, and their inputs are implicitly mapped into high-dimensional feature spaces for efficient nonlinear classification. A support vector machine constructs a hyperplane, or in a high or infinite dimensional space, which can be used for classification, regression, or hyperplanes set in other tasks. A good separation is achieved by a generalization of a hyperplane with a maximum distance to the closest training data point of any class, due to the generalization error of the classifier under a large margin. While the original problem may be described in a finite dimensional space, it often happens that the discriminating set is linearly separable in that space. For this reason, it has been suggested that mapping the original finite dimensional space to a much higher stereo space makes it easier to separate in space. Keeping the computational load reasonable, the mapping using the SVM scheme is designed to ensure that the dot product can be easily calculated in terms of variables in the original space, by defining the calculation of the kernel function k(x, y) selected among them to accommodate problem. A hyperplane in a high dimensional space is defined as the dot product of a set of points and the vector in that space is constant. The defined hyperplane carrier can be selected to linearly combine an image of the feature vector based on the data occurring in the parameter alpha_i. This choice of a hyperplane in which the feature space of x is mapped to the hyperplane is defined by the relationship: glytype sum_ialpha_ik (x_i, x) = mathrm {constant}. Note that if k(x, y) becomes smaller as x increases further away from x, the degree of the corresponding data base point x_i of the proximity of the test point x is measured at each of the summations. In this way, the sum above the kernel can be used to measure the relative proximity of the individual test points to the data points originating in one or the other set to be identified. SVM classifier classification: 1) Linear classifier: A linear function that can be used for linear classification. One advantage is that no sample data is needed. The linear classifier formula is as follows: --(1) 2) Nonlinear classifier: supports linear classification and nonlinear classification. Part of the sample data (support vector) is required, which is the data of αi≠0. The nonlinear classifier formula is as follows: Brushless DC Permanent Magnet Gear Motor Brushless Dc Motor,Brushed Dc Motor,Industrial Machine Dc Motor,Brushless Dc Permanent Magnet Gear Motor NingBo BeiLun HengFeng Electromotor Manufacture Co.,Ltd. , https://www.hengfengmotor.com